ML4Sci #11: Embedding Physical Domain Knowledge in Bayesian Networks for PV Process Optimization; DL for inverse design of EM metastructures; Deep elastic strain engineering of bandgaps
ML4Sci #11: Embedding Physical Domain Knowledge in Bayesian Networks for PV Process Optimization; DL for inverse design of EM metastructures; Deep elastic strain engineering of bandgaps
A tour of ML 4 Optics, and why it matters
Hi, I’m Charles Yang and I’m sharing (roughly) weekly issues about applications of artificial intelligence and machine learning to problems of interest for scientists and engineers.
If you enjoy reading ML4Sci, please hit the ❤️ button above. Or forward it to someone who you think might enjoy reading it!
As COVID-19 continues to spread, let’s all do our part to help protect those who are most vulnerable to this epidemic. Wash your hands frequently (maybe after reading this?), check in on someone (potentially virtually), and continue to practice social distancing.
Thought of this during my most recent group meeting and thought someone here might appreciate it:
Embedding physics domain knowledge into a Bayesian network for PV process optimization
Published on January 13, 2020
Process optimization is an important scaling step between fundamental research and mass-production. While traditional techniques include grid search, particle swarm optimization, and bayesian optimization, they often lack interpretable explanations of root causes of underperformance. This work out of Tonio Buonassisi’s group at MIT (who also has a great, free MIT OCW course on photovoltaics) and the National University of Singapore uses a bayesian neural network to speed up inference and understand the mapping between process variables, material descriptors and performance for GaAs solar cells. Specifically, this work optimizes the growth temperature profile of GaAs in a metal organic chemical vapor deposition (MOCVD) process.
This work also demonstrates how inserting ML in different places of an optimization pipeline can provide an overall speedup. A surrogate neural network model is used to speed up PDE calculations that map material descriptors to experimental measurements. A bayesian neural network is used to map the process variable (growth temperature) to material descriptors, which allows both the encoding of physical priors and understanding relationships between process variable and descriptor. Rather than directly black-boxing from process variable to target variable and running optimization, this work breaks up optimization into several steps and uses different neural network architectures to get both speedup and interpretability. By using bayesian neural networks, they demonstrate both interpretable mappings between process and descriptors and are able to encode physical priors distributions e.g. temperature to bulk doping levels follows an arrhenius equation.
This work not only uses the bayesian neural network to map between process variables and material descriptors, it also experimentally verifies these trends (see Fig. 4 in the paper). The authors also experimentally synthesize the optimized GaAs solar cell and demonstrate a relative 6.5% improvement in photovoltaic efficiency from the baseline.
Deep Learning for inverse design of EM nanostructures
Published on February 04, 2020
This paper has a solid introduction section, which I think gave a good overview of inverse design problems and why many-to-one inverse mappings are challenging. They argue that rather than using faster surrogate models or better optimization algorithms, the trick is to change mappings from many-to-many design-to-response problems into a latent one-to-one mapping via autoencoders (see figure below).
The innovative use of deep autoencoders is further evidence of how ML4Sci problems force practitioners to use standard deep learning tools in different ways. The following work mixes and matches different parts of encoder-decoders type architecutres to different latent/experimental spaces (see Fig 5. in the paper), which I outline here. For reference, the forward problem is mapping design parameter(A) -> optical response(B) while the inverse problem is optical response(B) -> design parameter(A).
optical response (B) -> latent, compressed optical response (B’) -> original optical response (B)
Design parameters (A) -> latent, compressed design parameters (A’) -> latent, compressed optical response (B’)
Translate step 2. to original optical response (B) by using the decoder in step 1.
For extracting inverse design rules, take optical response (B) -> latent, compressed optical response (B’) -> latent, compressed, design rules (A’)
This methodology is applied to nanophotonic metasurface design, specifically one with gold nanoribbons on top of an optical phase change material, GeSbTe, which has applications for smart windows and radiative cooling.
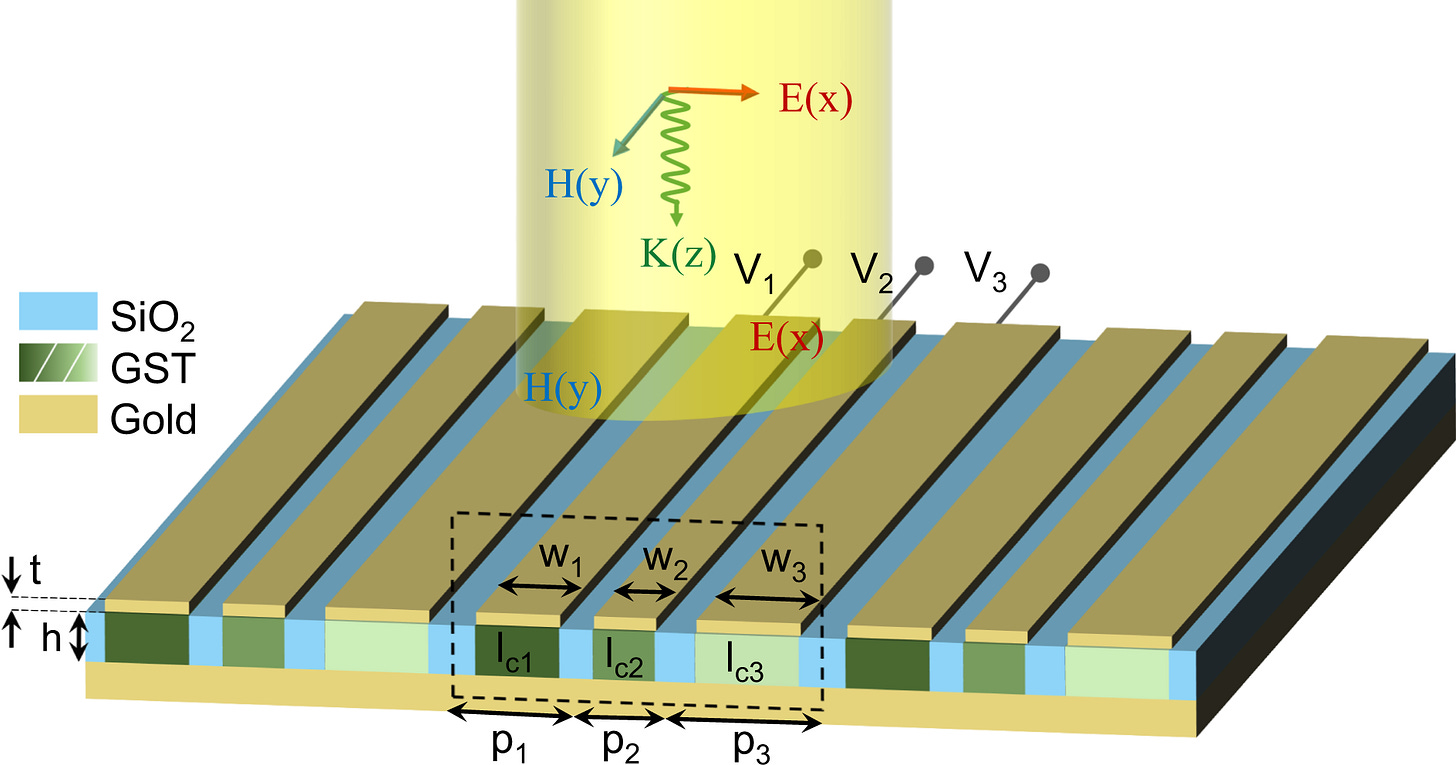
Using the autoencoder, the authors gain physical intuition about the importance of various design parameters, particularly that the height of the nanoribbon is the dominant feature. They also demonstrate that their methodology is able to identify designs with good infrared reflection, which is important for radiative cooling applications.
[paper]
Deep elastic strain engineering of bandgap through ML
Published on February 15, 2019
Nanoscale materials often exhibit non-intuitive and extreme properties compared to their bulk counterparts. The explosion of complexity makes this field attractive for engineering next-gen materials, but also for AI to help with materials design and discovery. One property of nanoscale materials is that they can withstand much higher elastic strain than their bulk counterparts. This mechanical strain also results in optical property changes as a result of the shift in the underlying density of states. For instance, the semiconductor industry has been using strain engineering to improve computer processor speeds since the mid-2000’s, as strain engineering can also be used to tune charge mobility.
However, engineering the strain tensor (which is 6D) to achieve some desired property change, in this case, the optical bandgap, is a high-dimensional and difficult problem. This work also highlights a common problem, particularly in chemical ab initio quantum calculations: they have 2 numerical models, one fast and inaccurate, the other slow and accurate. Building off of previous work, they use two neural networks to fuse the datasets together. They map out the predicted momentum space of the DOS and compare it to known theory. A nice work that highlights how deep learning can be used to explore high-dimensional spaces to enable a growing technique in semiconductor engineering.
[pdf]
ML 4 Optics
This issue coincidentally highlights 3 articles that all use deep learning for optical property manipulation (PV processes, nanophotonic metasurfaces, strain engineering bandgap). I thought this would be a good chance to highlight some aspects of this field that make it well-suited to ML (as opposed to some fields which face intrinsic difficulties). As I’ve written about elsewhere, there are several characteristics which make a scientific field amenable to ML.
a culture of open-sourcing datasets
it’s ok to be wrong computationally as long as you’re right experimentally
believable numerical models or high-throughput experimental methods
data that can be easily represented in ML models
there exist problems that are intractable with current methods
1. and 2. are directed at high-risk fields or those with sensitive data e.g. healthcare, power grid operators. 3. is for fields that lack strong numerical models that describe phenomena e.g. cellular biology, but this can sometimes be compensated with tons of experimental data e.g. genomics, or even literature review for material science (see ML4Sci #1). The study of light-matter interaction has a lot going for it: Maxwell equations and efficient software implementations of those equations are well-known; experimental methods exist to verify simulations; and an explosion of complexity at the nano and microscale results in large design spaces that can only be efficiently explored with AI. Owen Miller’s Ph.D thesis, which I covered in ML4Sci #9, also covers similar ground for why optics and EM are ripe for ML exploration. Can you think of other fields that fit these criteria well, or perhaps other criteria for ML4Sci? Drop it in the comments 💬 !
In the News
US Patent and Trademark Office rules that AI systems cannot be listed as inventors in patents
Dept. of Defense releases AI primer for non-technical managers
Lessons learned from attending the virtual ICLR conference
Google uses ML to understand yeast gene expression[paper][blog][commentary]
COVID-19 breaks AI systems in retail, finance
Microsoft and Intel team up: convert binary code to images and use deep learning to classify malware
Thanks for Reading!
I hope you’re as excited as I am about the future of machine learning for solving exciting problems in science. You can find the archive of all past issues here and click here to subscribe to the newsletter.
Have any questions, feedback, or suggestions for articles? Contact me at ml4science@gmail.com or on Twitter @charlesxjyang